We then learned about rotational inertia. Rotational inertia is the property of rotating objects to stay at rest or stay in motion. It is very similar to linear inertia, which we learned about in the beginning of the year. One key difference however, is that linear inertia depends highly on the mass of the object. While rotational inertia depends on the distribution of mass throughout the object. If an object has its mass distributed evenly throughout, it will have less rotational inertia than one with the mass concentrated far from the axis.
One question constantly asked to utilize this property is as follows: What will win in a downhill race? A bowling ball, or a volleyball.
The answer is a bowling ball, which seems very unlikely to someone who has not studied physics yet. This is because the bowling ball has alot of mass, and it is distributed evenly throughout. The volleyball is filled with air, and is surrounded by a rubber sphere. This concentrates all the mass outward. Therefore, the bowling ball has less rotational inertia, and will be easier to get rolling, and will ultimately win the race. (Nice try physics!)
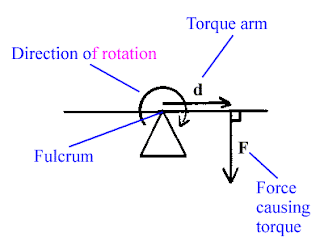
Next, we learned all about torque. Torque is what causes rotating objects to stop or move. We already learned that outside forces either impede or increase the motion of moving objects. Well, torque is that outside force for rotating objects. Torque has two key components: the lever arm, and the force. In order to have a large torque, you can increase the length of the lever arm, or simply apply more force. Also, the lever arm must be perpendicular to the object you are trying to move. The following diagram is a good representation of torque.
We then moved on the Centripetal and Centrifugal force. Centripetal force is the force that causes an object to move towards the center of rotation, such as when a car rounds a curve. Centrifugal force is what we humans conceive to be the force that pushes us away from the axis of rotation. However, centrifugal force is not real. One instance of people falsely bringing up centrifugal force is when a car rounds a curve, and the person in the passenger seat feels pushed towards the door. This is not the work of a force. It simply shows the passenger's inertia at work. It is actually the door that hits the person, but, due to Newton's 3rd Law which states that for every action there is an equal and opposite reaction, the person applies force to the door.
One example of centripetal force is the orbiting of planets. The moon, for example, is pulled towards the earth by the centripetal force known as gravity, and it continues to rotate around the planet. Without the centripetal force, it would float away into space.
This is an example of centripetal force at work in a roller coaster, as it makes a loop.
The final topic we discussed was angular momentum, or rotational momentum. Angular momentum is very similar to linear momentum. One way it is similar, is that it must be conserved. One example of this at work is when an ice skater goes to spin in the air, she brings her arms to her chest, as to decrease her rotational inertia. Since angular momentum is constant (must be said in every answer), her speed will increase, giving her more rotations and a better score.
Overall, this unit was not very challenging. The calculations were rather simple. I was mainly dealing with the equation for torque, setting it up and balancing it to find measures of forces. This unit relates greatly to the real world. For example, if you want to go very fast on a merry go round, you want to pick the horse farthest away from the axis of rotation, as to increase your tangential momentum.
